CFD(数値流体力学)では、流体の方程式であるNaver-Stokes方程式と連続の式を連立して解いて流速と圧力を計算しています。ここでNaver-Stokes方程式と連続の式は数学的には偏微分方程式と呼ばれる方程式の種類になります。微分方程式を簡単に言えばある量が変化するときの関数を求めることをいいます。流体力学を含む物理学での方程式はほとんどが微分方程式で記述されます。

Naver-Stokes方程式は

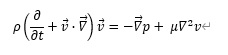
ここで、を表しており、流体力学での運動方程式になります。

連続の式は

 と表され、連続の式では流線上どの断面でも流量が一定であることを表しています。Navier-Stokes方程式と連続の式は解析的(手計算)な計算ができないためコンピュータを使ったCFDが使われます。

最後に一般相対性理論で扱われるEinstein方程式を紹介します。

Einstein方程式は

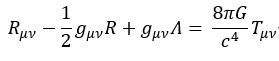
  ここで、

これまで近似的にEinstein方程式から完全流体(粘性係数0の流体)を仮定したフリードマン方程式など宇宙論に使われる解(ルメートル解、ド・ジッター解や反ド・ジッター解等)やブラックホール解(静的なブラックホールであるシュバルツシルト解、回転するブラックホールであるカー解、電気を持ったブラックホールであるライスナー・ノルドシュトリム解等)が計算されています。数学的には非線形な連立偏微分方程式と呼ばれるもので、曲率の項には実際には時空の曲がり具合(アフィン接続係数)の微分項が入っています。アインシュタイン方程式も厳密な解析解を求めるのは困難で、数値相対論と呼ばれるコンピュータを使った数値計算が行われます。